Sistemas Lineares
Sistemas Lineares são conjuntos de equações associadas entre elas que apresentam a forma a seguir:

A
chave do lado esquerdo é o símbolo usado para sinalizar que as equações
fazem parte de um sistema. O resultado do sistema é dado pelo resultado
de cada equação.
Os coeficientes amxm, am2xm2, am3xm3, ... , an, an2, an3 das incógnitas x1, xm2,xm3, ... , xn, xn2, xn3 são números reais.
Ao mesmo tempo, b também é um número real que é chamado de termo independente.
Ao mesmo tempo, b também é um número real que é chamado de termo independente.
Sistemas lineares homogêneos são aqueles cujo termo independente é igual a 0 (zero): a1x1 + a2x2 = 0.
Portanto, aqueles que apresentam termo independente diferente de 0 (zero) indica que o sistema não é homogêneo: a1x1 + a2x2 = 3.
Portanto, aqueles que apresentam termo independente diferente de 0 (zero) indica que o sistema não é homogêneo: a1x1 + a2x2 = 3.
Classificação
Os
sistemas lineares podem ser classificados conforme o número de soluções
possíveis. Lembrando que a solução das equações é encontrado pela
substituição das variáveis por valores.
- Sistema Possível e Determinado (SPD): há apenas uma solução possível, o que acontece quando o determinante é diferente de zero (D ≠ 0).
- Sistema Possível e Indeterminado (SPI): as soluções possíveis são infinitas, o que acontece quando o determinante é igual a zero (D = 0).
- Sistema Impossível (SI): não é possível apresentar qualquer tipo de solução, o que acontece quando o determinante principal é igual a zero (D = 0) e um ou mais determinantes secundários são diferentes de zero (D ≠ 0).
As
matrizes associadas a um sistema linear podem ser completas ou
incompletas. São completas as matrizes que consideram os termos
independentes das equações.
Os sistemas lineares são classificados
como normais quando o número de coeficientes é o mesmo que o número de
incógnitas. Além disso, quando o determinante da matriz incompleta desse
sistema não é igual a zero.
Exercícios Resolvidos
Vamos resolver passo a passo cada equação a fim de classificá-las em SPD, SPI ou SI.
Exemplo 1 - Sistema Linear com 2 Equações

Exemplo 2 - Sistema Linear com 3 Equações
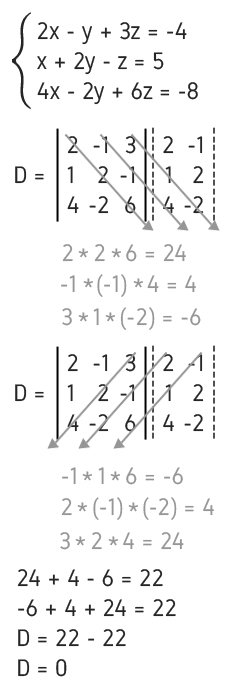
Se
D = 0, podemos estar diante de um SPI ou de um SI. Assim, para saber
qual a classificação correta, vamos ter de calcular os determinantes
secundários.
Nos determinantes secundários são utilizados os
termos independentes das equações. Os termos independentes substituirão
uma das incógnitas escolhidas.
Vamos resolver o determinante secundário Dx, por isso, vamos substituir o x pelos termos independentes.

Como
o determinante principal é igual a zero e um determinante secundário
também é igual a zero, sabemos que esse sistema é classificado como SPI.
https://www.todamateria.com.br/sistemas-lineares/



Nenhum comentário:
Postar um comentário